振動式物位開關在過去幾十年得到長足發(fā)展,在振動式音叉液位開關的設計中,其音叉振動幅度一般很小,但振動頻率較高,一般在1200Hz左右。音叉液位開關采用壓電器件實現(xiàn)叉體的振動驅動與檢測。當叉體與被測液體接觸時,因阻尼使叉體的諧振頻率明顯降低,振動頻率的變化直接反應在壓電檢測器件的輸出信號上,檢測電路對頻率的變化進行判別并輸出一個開關信號。
因此,在音叉液位開關設計過程中,分析當其接觸被測液體時,其振動特性和變化規(guī)律,就顯得尤為重要,而影響或改變音叉振動特性的因素就是介質產生的阻尼。那么,振動式音叉液位開關的阻尼是怎樣的呢?
阻尼的相關概念
在對振動式音叉液位開關的阻尼進行分析之前,我們先來看看阻尼的概念。
阻尼,是阻尼是一種能量耗散機制,是指任何振動系統(tǒng)在振動中,由于外界作用或系統(tǒng)本身固有的原因引起的振動幅度逐漸下降的特性,以及此一特性的量化表征。根據(jù)不同類型阻尼的物理機制及具體的阻尼現(xiàn)象,或者為了數(shù)學計算的方便,物理學家和工程專家在實驗的基礎上,相繼建立了許多描述阻尼力的數(shù)學模型。在單自由度有阻尼體系運動方程的基礎上,用來描述阻尼常見的三種數(shù)學模型分別是粘性阻尼、遲滯阻尼和結構阻尼。
粘性阻尼假定阻尼力與速度成正比,其阻尼力表示為F=-CV。方便地表達阻尼對頻率、共振等的影響,是應用最為廣泛的阻尼模型,通過將阻尼系數(shù)與結構體系的質量、剛度相聯(lián)系,可以方便地構造出具體的阻尼系數(shù),是目前最常用的阻尼表達方法。粘性阻尼很好地描述了在粘性流體中運動所受到的阻尼作用。
遲滯阻尼又稱頻率相關阻尼,它與粘性阻尼系數(shù)C相對應的阻尼因子是h/θ,其阻尼力表示為F=(h/θ)×V,其中h為材料遲滯阻尼常數(shù);θ為振動頻率。砂子的阻尼特性可很好地用遲滯阻尼模型來描述。
結構阻尼理論認為,在固體材料中,阻尼力獨立于應變速度,而與應變幅值有關。結構阻尼能很好地描述固體材料的阻尼特性。
振動式音叉液位開關的阻尼分析
振動式物位開關中的音叉液位開關在流體介質中做單自由度的簡諧振動,其所受到的阻尼模型視為粘性阻尼模型。由牛頓第二定律,即F=ma,得到其阻尼體系運動方程為:
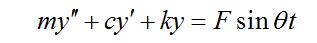
其中介質對音叉振動的阻尼力即為:
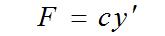
C稱為阻尼系數(shù),單位為N.s/m,c與物體的形狀、尺寸及介質的性質(如密度、溫度、壓力、粘度等)有關;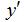 為振動速度V。事實上,介質對振動的阻尼力的影響因素并不是單一的,可以肯定的是,阻尼力的大小和振動的速度、介質密度、接觸面積都相關,此外,還與振動頻率及振幅有關聯(lián)。在流體介質中,阻尼力大小還與粘度系數(shù)有關。在接觸面積逐漸增大時,振動速度和振幅都會衰減,阻尼系數(shù)c也會隨之減小,它是一個不斷變化的量。(文章摘自:http://www.levelmeter.cn/yfshow-23-276-1.html,轉載請注明出處。)
為振動速度V。事實上,介質對振動的阻尼力的影響因素并不是單一的,可以肯定的是,阻尼力的大小和振動的速度、介質密度、接觸面積都相關,此外,還與振動頻率及振幅有關聯(lián)。在流體介質中,阻尼力大小還與粘度系數(shù)有關。在接觸面積逐漸增大時,振動速度和振幅都會衰減,阻尼系數(shù)c也會隨之減小,它是一個不斷變化的量。(文章摘自:http://www.levelmeter.cn/yfshow-23-276-1.html,轉載請注明出處。)

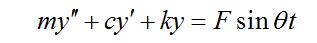
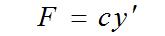
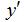 為振動速度V。事實上,介質對振動的阻尼力的影響因素并不是單一的,可以肯定的是,阻尼力的大小和振動的速度、介質密度、接觸面積都相關,此外,還與振動頻率及振幅有關聯(lián)。在流體介質中,阻尼力大小還與粘度系數(shù)有關。在接觸面積逐漸增大時,振動速度和振幅都會衰減,阻尼系數(shù)c也會隨之減小,它是一個不斷變化的量。(文章摘自:
為振動速度V。事實上,介質對振動的阻尼力的影響因素并不是單一的,可以肯定的是,阻尼力的大小和振動的速度、介質密度、接觸面積都相關,此外,還與振動頻率及振幅有關聯(lián)。在流體介質中,阻尼力大小還與粘度系數(shù)有關。在接觸面積逐漸增大時,振動速度和振幅都會衰減,阻尼系數(shù)c也會隨之減小,它是一個不斷變化的量。(文章摘自: